高中数学中求最小值的方法（通过数学推导和应用解决最小值问题）
在高中数学中，求解最小值是一个常见的问题，它涉及到优化和极值的概念。通过数学推导和应用，我们可以找到一个函数的最小值。本文将介绍一些常用的方法和技巧，帮助读者更好地理解和解决最小值问题。
1.最小值与极值的概念及关系
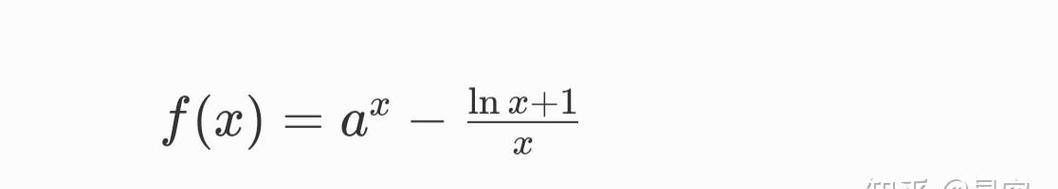
极值是一个函数在定义域内取得的最大值或最小值，其中最小值即为函数的最小值。通过分析函数的导数和图像，我们可以确定极值点以及最小值点的位置。
2.一元函数求最小值的常用方法
利用一元函数的导数求解最小值是一种常见的方法。通过求导，我们可以找到函数的临界点并判断其是否为最小值点。
3.多元函数求最小值的技巧与策略
多元函数的求最小值相对复杂一些。我们可以利用偏导数和拉格朗日乘子法来解决多元函数的最小值问题。
4.最小二乘法在实际问题中的应用
最小二乘法是一种常见的统计方法，用于处理由于测量误差而产生的数据拟合问题。它可以通过最小化误差的平方和来找到最佳拟合曲线或平面。
5.利用数学模型解决实际问题中的最小值问题
在实际问题中，我们经常需要建立数学模型来描述某个系统或过程。通过对模型进行优化，我们可以找到系统的最优解，即最小值。
6.最小值问题与约束条件
在一些问题中，我们需要考虑一定的约束条件，如资源限制、等式或不等式限制等。通过引入约束条件，我们可以将问题转化为带有约束条件的最优化问题，求解其最小值。
7.动态规划方法求解最小值问题
动态规划是一种递推求解最优化问题的方法。通过将原问题分解为若干子问题，并记录子问题的解，我们可以逐步推导出最终的最小值。
8.最小生成树算法在网络优化中的应用
最小生成树算法是一种常用于网络优化的算法。通过选择权重最小的边构成一个连通图，我们可以找到一棵最小生成树，表示网络中的最优路径。
9.线性规划方法求解最小值问题
线性规划是一种常用的最优化方法，用于解决一些具有线性约束条件的最小值问题。通过构建线性规划模型，我们可以通过求解线性规划问题得到最小值。
10.最优化算法在机器学习中的应用
机器学习中的很多问题可以转化为寻找一个函数的最小值。通过使用梯度下降等最优化算法，我们可以训练出最优的机器学习模型。
11.最小值问题中的数值计算与优化算法
在实际计算中，我们往往需要借助数值计算方法和优化算法来求解最小值问题。例如，牛顿法、拟牛顿法等都是常用的数值优化算法。
12.对称性与最小值问题
一些函数具有对称性，如偶函数、周期函数等。通过利用函数的对称性，我们可以简化最小值问题的求解过程，减少计算量。
13.凸函数与最小值问题
凸函数是一类特殊的函数，具有很多良好的性质。通过研究凸函数的性质，我们可以更容易地求解凸函数的最小值。
14.求解最小值问题中的应用举例
通过实际应用的案例，我们可以更加直观地理解最小值问题的解决方法。例如，最小切割问题、最短路径问题等。
15.与展望
通过对高中数学中求解最小值的方法进行介绍和探讨，我们可以看到数学在解决实际问题中的重要性。未来，随着数学理论和计算方法的不断发展，我们相信在求解最小值问题方面会有更多的新技术和方法出现。
本文从一元函数到多元函数，从数学模型到最优化算法，系统介绍了高中数学中求解最小值的方法和应用。希望读者通过本文的阅读，能够更好地理解和掌握这些方法，进一步提高数学问题的解决能力。
- 腾龙电影的镜头如何打造出精彩视觉效果（剖析腾龙电影的镜头运用技巧和创新思维）
- 磁铁的磁性魅力（探索磁铁的神奇特性与应用）
- 以NF定制耳机（以NF定制耳机的质量、样式、音质及舒适度一览）
- 创新AurvanaLive2（探索未知领域，体验非凡音效）
- 以轰天雷X8NX3S为主题的全面评测（性能超群的X8NX3S让你爱不释手）
- U2音响（探索U2音响的卓越品质和出色性能）
- i32330m处理器（深入解析i32330m处理器的性能和优势）
- 探索索尼a7m2k套机的卓越表现与功能（一款专业级全画幅相机的实力与优势）
- 魅族M463C手机真的那么好吗？（细数魅族M463C的亮点与不足）
- 中兴2A手机全面评测（性价比超高，适合日常使用）
- 中兴智慧语音（领先技术助力智能语音发展，引领智慧生活新时代）
- 以看尚智能电视怎么样为主题的产品评测（通过用户体验评价以看尚智能电视的性能和功能是否满足需求）
- 以影驰名人堂的魅力与荣誉（致敬电竞世界的巨星和传奇）
- HTCVive（探索虚拟现实世界的奇妙之旅）
- 小米2空气净化器的功效和优势（呼吸新鲜空气，让家居环境更健康）
- 三星手机摄像头表现如何？（探究三星手机摄像头的特点和性能）
